带孔弹性元件温度场的模拟实验方法

张卫民那荣起亚·康·尼基金

1 引言

带孔弹性元件在测力与称重等领域有着广泛应用。在一些特殊场合，如火箭发射、冶金生产等测控设备中作为基础件应用时，常要处于不均匀温度场中而产生热应力，从而带来测量误差。为消除这种误差，必须采取相应的补偿措施。这就要求对带孔弹性元件在局部热影响下的温度及应力分布状态进行研究。

计算机技术的迅猛发展极大促进了有限元、边界元等数值方法的完善，从而使得如带孔弹性元件的温度场、应力场分析这类理论上可以归结为平面问题的数值模拟变得轻而易举。与此相比，采用实验方法研究温度和应力问题则显得有些陈旧和费时费力。但即便如此，实验方法仍有其独特优势，首先，它可以为数值计算结果提供验证手段，因为数值计算中若参数选择不当或数学模型有偏差，仍会出现较大误差；其次，计算因受计算机和软件等条件的制约而常常无法展开，实验则因设备和条件要求不苛刻而容易实现。

确定温度场是研究热应力的前提条件，因篇幅所限，本文仅讨论弹性元件在局部稳态热影响下的温度场实验研究方法。

2 实验研究的基本方法简介

2.1 实验研究的理论基础

根据光弹性实验基本理论，在平面应变状态下，弹性元件和实验模型的热应力间具有如下关系［1］：

分别以下标“H”、“M”表示弹性元件和模型，式中，σH、σM—分别表示弹性元件和模型的热应力；EH、EM—二者的弹性模量；αH、αM—热膨胀系数；υH、υM—泊松系数；△TH、△TM—温度差。

在弹性远件和模型上得到稳定的应力状态的最短时间之比为［1］

式中，CH、CM—比热容；ρH、ρM—材料密度；lH、lM—弹性元件和模型的相应尺寸。

以上公式表明，在材料性能参数已知且满足热平衡条件的情况下，可用模型研究弹性元件的热应力状态。

2.2 材料选择与模型制作

模型材料选择厚度为8mm的树脂材料3Д－6M，按与元件成相似关系的几何尺寸经机械加工方法制成［2］，应注意保持小的加工余量以防止模型上残余应力过大。做好的模型需放入保温炉中进行24小时的退火处理，以有效消除残余应力。加热器是用3Д－6M材料做骨架，以细铜丝缠绕而成，在细铜丝两端加可调电压，即可达到加热并改变温度的目的。

2.3 热电偶的制备与标定

热电偶是由直径为0．33mm的细铜丝和直径为0．4mm的康铜丝在40V电压和96%的酒精中焊接而成。在使用前，需对所制成的热电偶进行标定，其标定装置如图2—1所示。

1－热电偶测量端；2－盛有机油的加热容器；3－可调变压器；4－伏特计；
5－水银温度计；6－换位开关；7－指针式万用表；8－盛有冰水混合物的容器

将热电偶的热端（测量端）放入盛有机油的容器2中，冷端（补偿端）放入盛有冰水混合物的容器8中，油温控制通过调节变压器3改变容器2温度来实现，而电压值则由伏特计4读出，油温由水银温度计5读出，热电偶的温度由指针式万用表7读出，拨动换位开关就可以读出多个热电偶的示值。

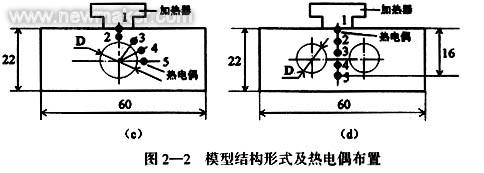
对制备的热电偶在20℃～80℃范围内进行3次重复标定，取其平均值利用最小二乘法进行数值拟合，得回归方程

T＝2．4＋2．59 V

式中T为温度值，V为电压值。在上述温度范围内，标定曲线为一理想直线。

2.4 温度场的确定

实验选择带孔弹性元件的关键部位进行研究，在模型上布置一系列热电偶，以研究温度场的分布情况，其结构及热电偶布置如图2—2所示。图2—2a研究模型沿高度方向温度分布和模型长度B之间的关系；图2—2b研究模型沿长度方向温度分布和模型高度B之间的关系；图2—2c研究单孔模型沿圆周方向温度分布和孔径D之间的关系；图2—2d研究双孔模型沿高度方向温度分布和孔径D之间的关系。

确定模型温度场的实验装置如图2—3所示，模型加热区宽度为20mm，加热区表面的温度为70℃，且温度保持时间为20min以上，此时热电偶读数再不发生任何变化，认为所研究的模型温度场为稳态温度场，且边界上作用有局部热源，模型的边界条件属于对流换热。这里仅考虑二维问题，忽略了模型两侧面换热，会给实验带来一定误差。该实验方法与理论计算结果的对比已有叙述［1］，故此处不再说明。整个实验在室温恒定（20℃），空气流通不大的房间内进行。

实验结果数据经最小二乘法拟合处理，得如下形式

式中，Tx—模型上距加热区距离为x处的温度值：
T∞—距离加热区无穷远处温度值，这里取环境温度20℃。

根据实验数据加工整理的部分结果如表2—1所示，其中B、D为模型几何参数，k为回归方程的指数项参数、η、mη分别为回归方程的置信度和平均拟合误差。

3 结束语

本文中所讨论的实验模拟方法，可作为研究各种复杂形状弹性元件二维温度场模拟实验研究的一般性方法。

参考文献
［1］AJIEKcaHдP A．Я.,AXMeT3ЯHOB M.X.ПOJIЯPN3aUNOHHO-OПTNчeckNe MeTOTbbI MexaHNKN дeфOPMNPyeMOгO Teлa[M].-M.:Hayka,1973,676c.
［2］ПPNгOPOBCKNй H.M.,ПPeйcc A.K.,N.T.д．MOдeJIN N3 HOBOгOOп TNчeckN akTNBHOгO MaTePNaJIa дляпOJIяPN3aцNOHHO OпTNчeckoro MeTOдa NCCдeдOBaHNя HaпPяжeHNй［C］．－M．：N3дBOфNл．BNHNTN,-1958-156C.
［3］БeляeB H.M.PядHO A.A.MeTOдbI TeOPNN TeплопPOBOдHOCTN［M］．－M．：Bbicшaя шkOлa，1982，327c

张卫民1 那荣起1 亚·康·尼基金2
1．北京理工大学，北京100081；2．乌克兰基辅国立技术大学仪器制造系

相关栏目

最新文章

热门文章